안녕하세요. 오늘은 구에 텍스처를 입힐 때, 발생하는 계단현상에 대해 알아보겠습니다.
이번 글의 소스는 RayTracing in one week이라는 아티클을 기반으로 하고 있습니다.
아티클 전체를 다루기는 어려우므로, 이번 글에서는 이 챕터의 4.3을 봐주시면 감사하겠습니다.
https://raytracing.github.io/books/RayTracingTheNextWeek.html#texturemapping/solidtextures:acheckertexture
(point3(min.x(), min.y(), min.z()), dx, dz, mat)); // bottom return sides; } ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ [Listing [box-class]: [quad.h] A box object] Now we can add two blocks (but not ro
raytracing.github.io

이번 예제에서 사용할 텍스처입니다.
이미지를 직접 import해서 사용하실 수도 있지만,
저는 procedural generation(코드로 이미지를 생성)하는 방식을 사용했습니다.

체크보드 텍스처를 정육면체(cube)에 매핑할 경우, 다음과 같은 결과를 얻게됩니다.
하지만 큐브가 아니라 구(sphere)에 사용한다면 어떻게 될까요?

color value(double u, double v, const point3& p) const override
{
auto xInteger = int(std::floor(inv_scale * p.x()));
auto yInteger = int(std::floor(inv_scale * p.y()));
auto zInteger = int(std::floor(inv_scale * p.z()));
bool isEven = (xInteger + yInteger + zInteger) % 2 == 0;
return isEven ? even->value(u, v, p) : odd->value(u, v, p);
}위 코드에서는 u,v를 사용하지 않고, point position의 좌표합이 2의 배수냐 아니냐에 따라 검은색/흰색으로 나누어 칠합니다.
예컨대 p=(0,0,0)이면 (0+0+0)%2==0이므로 검은색
p=(0,0,1)이면 (0+0+1)%2==0이므로 흰색
그런데, 이것을 구면에 칠하니까 다음과 같은 결과가 나왔습니다.



(1)(x+y)%2==0
(2)(x+z)%2==0
(3)(y+z)%2==0
자세히 보면 y component가 포함된 경우 , 원형 모양의 불규칙한 패턴이 추가됨을 알 수 있습니다.
2번 사진을 보면, x+z일때는 정상적으로 매핑이 동작하는 것을 확인했습니다.

x만 이용해서, xInteger의 값이 변함에 따라 stripe pattern을 칠했습니다.

y component만을 렌더링 했을때, x+y+z에서 발견한 계단현상을 발견했습니다.
왜 계단현상이 발생하는가?
텍스처의 생성 방식은 Integer%2==0을 체크하는 방식입니다.
여기서 Integer는 특정 axis 방향이 주어졌을때, 해당 방향으로 정해진 amount만큼 modulo 연산을 합니다.
쉽게 말해서 같은 색으로 칠해진 영역은, Integer 값이 같은 영역입니다.

1차원일때 검은색으로 칠해진 영역은 Int%2==0인 영역입니다.
(영역인 이유는 floor(x=0.0~0.9xx)를 하게 되면 전부 0.0이 되기 때문입니다.)

2차원으로 확장하면, Grid Pattern을 만들 수 있습니다.

3차원으로 확장하면, 큐브에서는 다음과 같이 그려집니다.
큐브에서는 이러한 방식으로 매핑을 하는 것은 문제가 없습니다.
하지만 구는 평면이 아니라 곡면이기 때문에
같은 방식으로 매핑을 하면 다음과 같이 나옵니다.
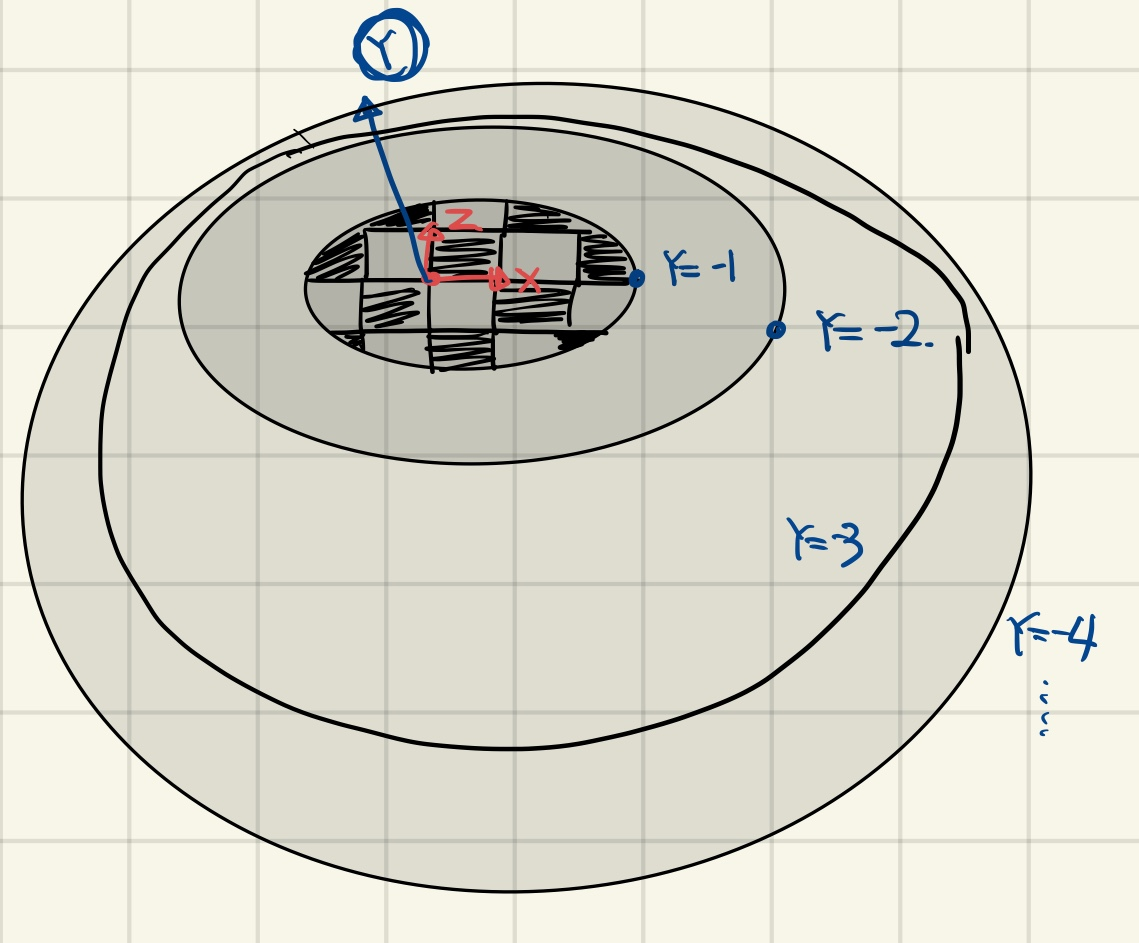
우선, 같은 영역, 그러니까 Y=0.0~0.99까지는 같은 패턴으로 그려집니다.
하지만 Y=[0.9,1.1] 구간에서는 Y=1.0~1.99로 값이 바뀝니다.
이때 Int(x+y+z)%2==0의 값이 깨지게 되면서, 두 구간(interval)사이에 불연속성이 생기는 것입니다.
[RayTracing in One Week]에서는
Spherical mapping이라는 방식으로 sphere위의 u,v좌표를 다시 계산합니다.
계산하는 과정은 article에 포함이 되어있으므로 적지는 않겠습니다.
그런데 특이점은 u,v를 계산해놓고 color를 계산할 때는 u,v가 사용되지 않았습니다.
그래서 u,v를 업데이트 한 이후에 렌더링을 하면 동일한 결과가 나옵니다.

이 계단 현상을 해결하기 위해, position이 아니라 uv좌표로 텍스처를 생성하도록 바꾸었습니다.
color value(double u, double v, const point3& p) const override
{
/*
auto xInteger = int(std::floor(inv_scale * p.x()));
auto yInteger = int(std::floor(inv_scale * p.y()));
auto zInteger = int(std::floor(inv_scale * p.z()));
bool isEven = (xInteger+yInteger+zInteger) % 2 == 0;
*/
auto uInteger = int(std::floor(u * inv_scale));
auto vInteger = int(std::floor(v * inv_scale));
bool isEven = (uInteger + vInteger) % 2 == 0;
return isEven ? even->value(u, v, p) : odd->value(u, v, p);
}inv_scale은 1/scale factor로, 패턴의 크기를 결정합니다.
여기서 p는 world position이고 사용자가 지정한 sphere의 위치와 radius에 따라 정해집니다.

그런데 u,v는 항상 [0.0,1.0] 사이의 값이므로 기존의 scale을 사용하면,
지나치게 촘촘한 결과가 나오게 됩니다.
사용해본 결과, scale*10배 정도면 적당하게 패턴이 보이는 것을 확인했습니다.

spherical mapping을 사용하면, 구의 pole에 가까워 질 수록 왜곡이 커지는 것을 확인할 수 있습니다.
'ComputerGraphics' 카테고리의 다른 글
| Chapter7. Implicit line representation (0) | 2023.02.06 |
|---|---|
| Interpolation-Based Animation (0) | 2022.11.14 |
| Smoothing a path (0) | 2022.11.11 |
| Working with paths (0) | 2022.11.09 |
| Interpolation of orientations (0) | 2022.11.09 |



댓글