This chapter presents method for precisely specifying the motion of objects. This chapter addresses how to use those basics to facilitate the production of computer animation. There is clear certainty about the positions, orientations, and shapes. Procedures and algorithms are used to be sure, but in a very direct manner in which the animator has specific expectations about the frame-by-frame motion. Later chapter cover "higher-level" algorithm in which the animator gives up some precision to produce motion with certain desired qualities.
4.1 Key-frame systems.
Many of the early computer animation systems were key-frame systems. Animator define and draw the key frames of the sequence to be animated. Assistant animators have the task of drawing intermediate frames by mentally inferring the action between the keys. The term key-frame has been generalized to apply to any variable whose value isst at specific key frames. These variables have been referred to in the literature as articulation variables, and the systems are referred to as track based. The animator can specify the key values and can control the interpolation curve by manipulaiting tangents or interior control points.

Because these animation systems keep the hand-drawn strategy of interpolating two-dimensional shapes, the basic operation is that of interpolating one curve into another curve. The interpolation is straightforward if the correspondence between lines in the frame is known so that each pair of lines can be interpolated on a point-by-point basis. This interpolation requires that for each pair orcurves the furves have the same number of points and that for each curve, the correspondence between the points can be established.
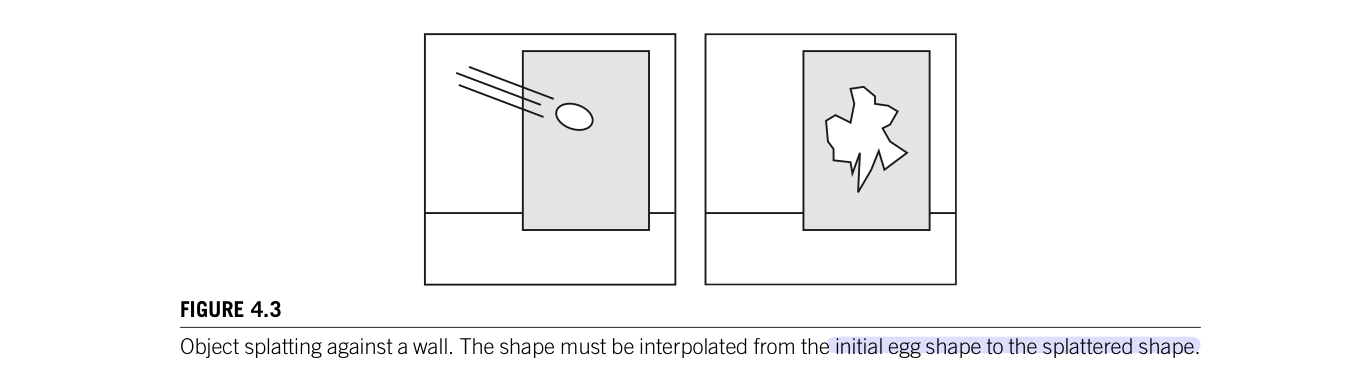
The simplest way interpolate the point is uisng linear interpolation. Point-by-point correspondence information is usually not known, the resulting interpolation is not necessarily what the user wants. The best one can expect is for the curve-to-curve correspondence to be given. The problem is to interpolate a curve as it should appear in intermediate frames. For example, observe the egg splatting against the wall.
Consider the simple case in which the key frames f1 and f2 consist of a single curve. The curve in frame f1 is referred to as P(u) and the curve in frame f2 is Q(v). This single curve mustbe interpolated for each frame. Without loss of generality, it is assumed that the curve is a generally vertical line in both key frames.
Some basic assumptions are used such as the fact that if the curve is a single continuous open segment in frame f1 and f2, then it should remain a single continuous open segment in all the intermediate frames. Also assumed is that the top point of P should interpolated to the top point in Q, and the bottop points should interpolate. P should interpolate to the entire curve Q; the mapping should be one-to-one and onto, also known as a bijection.
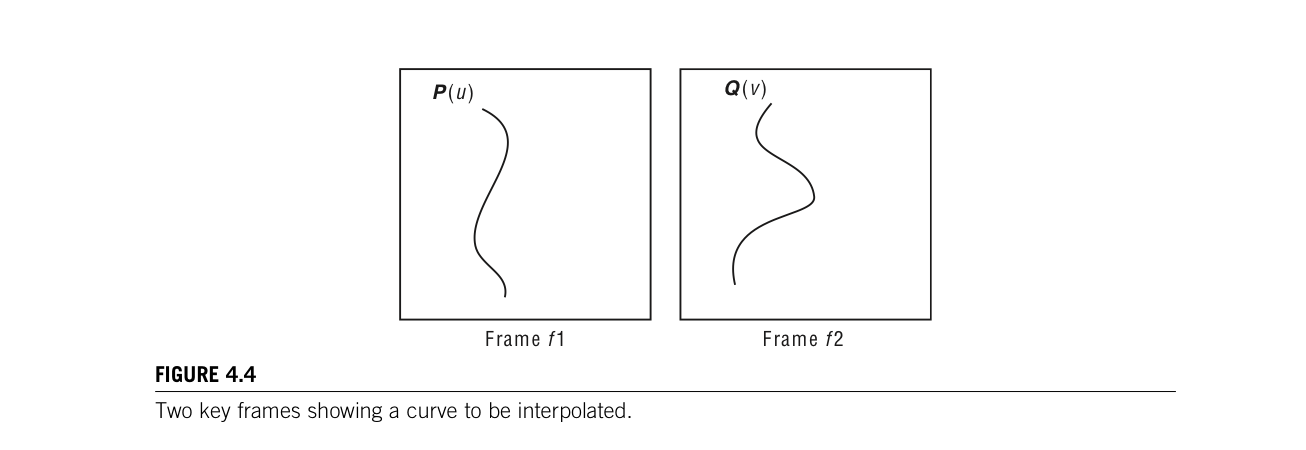
If both curves were generated with the same type of interpolation information, for example, each is a single cubic Bezier curve, then. Intermediate curves could be generated by interpolating the control points and reapplying the Bezier interpolation. Another alternative would be to use interpolating functions to generate the same number of points on both curves. These points could then be interpolated point-by-point basis.
Reeves proposes a method of computing intermediate curves using moving point constraints, which allows the user to specify more information concerning the correspondence of points and the speed of interpolation of those points. The basic approach is to use surface patch technology to solve problems of interpolating a line in time.
The first step is to define a segment of the curve to interpolate, bounded on top and bottom by interpolation constraints. Linear interpolation is used to bind the top and bottom segments. Next task is to define an intermediate curve based on the constraints. Typically applications of surface patch is used. For example, tangent information can be extracted from the curve definitions. The endpoint and tangent information can be interpolated along the top and bottom interpolation boundaries. These can be used to define an intermediate curve using Hermite interpolation.

'ComputerGraphics' 카테고리의 다른 글
| [RayTracing in One week]스피어 텍스처 매핑시 발생하는 계단현상 해결. (0) | 2025.04.07 |
|---|---|
| Chapter7. Implicit line representation (0) | 2023.02.06 |
| Smoothing a path (0) | 2022.11.11 |
| Working with paths (0) | 2022.11.09 |
| Interpolation of orientations (0) | 2022.11.09 |



댓글