2.2 Orientation representation
The best way to represent the position and orientation of an object and how to interpolate the represented informations over time to produce motion is a common issue in computer animation. A typcial scenario is, in two transformed states, to interpolate intermediate states, thus producing animated key-frame motion. Another scenario is when object is to undergo two or more successive transformation and it would be efficient to concatenate these transformation into a single representation. This section discusses possible orientation representations and identifies strengths and weaknesses. The next chapter addresses the best way to interpolate orientations. It is assumed that the final transformation applied to the object is a result of rotations and translations only, so that there is no scaling involved, nonuniform or the transformations considred are rigid body.
The first way to represent the orientation and position of an object is by a 4x4 transformation matrix. For example, a user specifies a series of rotations and translations. The series of transformation is complied into a compound 4x4 transformation matrix. In such a matrix, the upper left 3x3 submatrix represents a rotation to apply to the object, while the first three elemens of the fourth column represent the translation, the final 4x4 transformation matrix produced by multiplying all of the individual transformation matrices will result in a matrix that specifies the final position of the object by a 3x3 rotation matrix followed by a translation. The conclusion is that rotation can be interpolated independently from the translation.
Consider two such transformations that the user has specified as key states with the intention of generating intermediate transformations by interpolation. Interpolating the transformations is straightforward, but it is not at all clear how to go about interpolating the rotations. A property of 3x3 rotation matrices is that the rows and columns are orthonormal. Simple linear interpolations between the nine pairs of numbers that make up two 3x3 rotation matrices to be interpolated will not produce intermediate 3x3 matrices that are orthonormal and are therefore not rigid body rotations. It should be easy to see that interpolating from a rotation of 90 degrees about y-axis to a rotation of -90 degrees about the y-axis does not make sense.
So, direct interpolation of transformation matrices is not acceptable. There are alternative representations in performing such interpolation including fixed angle, Euler angle, axis-angle, quaternions, and exponential maps.
2.2.1 Fixed-angle representation
A fixed-angle rerpesentation refers to angles used to rotate about fixed axes. A fixed order of three rotations is implied, such as x-y-z. Orientation is given by a set of three ordered parameters that represent three ordered rotations about fixed axes. In fact, it is not necessary to use all three coordinate axes. For example, x-y-x is a feasible set of rotations. The only orderings that do nat make sense are those in which an axis immediately follows itself, such as in x-x-y. The main point is the orientation of an object given by three angles, such as (10,45,90). In this example, the orientation represented is obtained by rotating the object first about the x-axis by 10 degrees, then about the y-axis by 45 degrees and then about the z-axis by 90
the problem with using this scheme is that two of the axes of rotation can line up on top of each other when object can rotate freely in space.
Consider an object in an orientation represented by (0,90,0). A slight change in the first and third parameter will rotate the object slightly about the global z-axis because that is the rotation applied last to the data points. Note that change in first parameter will also have the effect of rotating the transformed object about the z-axis

The cause of this problem can often make interpolation between key positions problematic. Because of the 90-degree y-axis rotation, the object can no longer directly rotate about the x-axis.
2.2.2 Euler angle representation
In a Euler angle representation, the axes of rotation are the axes of the local coordinate system. A typical example of using Euler angles is found in the roll, pitch, and yaw of an aircraft. The Euler angle representation can use any of various orderings of three axes of rotation. Consider an x-y-z ordering specified as (a,b,c). The x-axis rotation is represented by Rx(a), and same above. Using a prime symbol to represent rotation about a rotated frame and remembering that points are represented as column vectors and are premultiplied by transformation matrices. Ry'(b)Rx(a). Using global axis rotation, the y-axis rotation around the rotated frame can be effected by Rx(a)Ry(b)Rx(-a)


2.2.3 Angle and axis representation
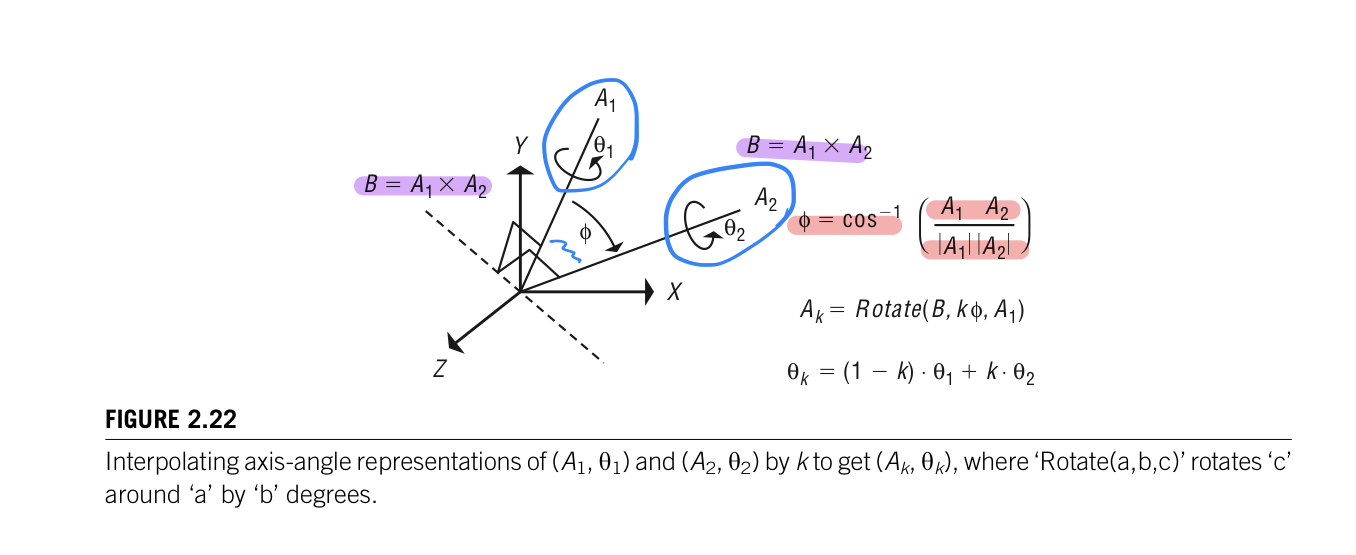
Leonhard Euler showed that one orientation can be derived from another by a single rotation about an axis. This is known as the Euler Rotation Theorem. Any orientation can be represented by three numbers:two for the axis, such as longitude and latitude, and one for the angle by a three-dimensional vector. Interpolation between representations (A1,theta1), and (A2,theta2) where A is the axis of rotation and theta is the angle, can be implemented by interpolating the axes of rotation and the angles separately. An intermediate axis can be determined by rotating one axis partway toward the other. The axis for this rotation is formed by taking the cross product of two axes A1 and A2. The angle between two axes is determined by taking the inverse cosin of the dot products of normalized versions of the axes. An interpolant, k can then be used to form an intermediate axis and angle pair.
'ComputerGraphics' 카테고리의 다른 글
| Interpolating Values (0) | 2022.10.31 |
|---|---|
| Quaternion representation (0) | 2022.10.27 |
| Error consideration (0) | 2022.10.24 |
| Homogeneous coordinates and the transformation matrix (0) | 2022.10.23 |
| Spaces and transformations (0) | 2022.10.18 |




댓글