[RayTracing in one week] Spherical mapping으로 구면에 텍스처 입히기

지난 글에서 소개했던 spherical mapping을 자세하게 설명하는 글을 만들었습니다.

이 책의 4.4 section에다가 조금 예시를 덧붙였습니다.

https://raytracing.github.io/books/RayTracingTheNextWeek.html#texturemapping/constantcolortexture

https://raytracing.github.io/books/RayTracingTheNextWeek.html#texturemapping/constantcolortexture

 

1. Cylindrical Mapping

1.1 Quad Mapping

이전의 큐브나 실린더를 렌더링 할 때는, 텍스처링할 평면을 QUAD로 가정했습니다.

물체 표면의 왼쪽 위를 texcoord=(0,0)으로, 오른쪽 아래를 (1.0,1.0)으로 두어서 텍스처를 매핑하는 방식입니다.

이 방식은, Quad에서 Quad로 매핑하는 방식이기 때문에, 특별한 왜곡이 발생하지 않습니다.

 

1.2 Cylinder Mapping

그 다음은, 실린더를 생성해 보도록 하겠습니다. 이번 예제에서 사용한 실린더의 경우 옆면만 생성했습니다.

(윗면도 cos과 sin을 이용해서 쉽게 생성할 수 있습니다.)

 

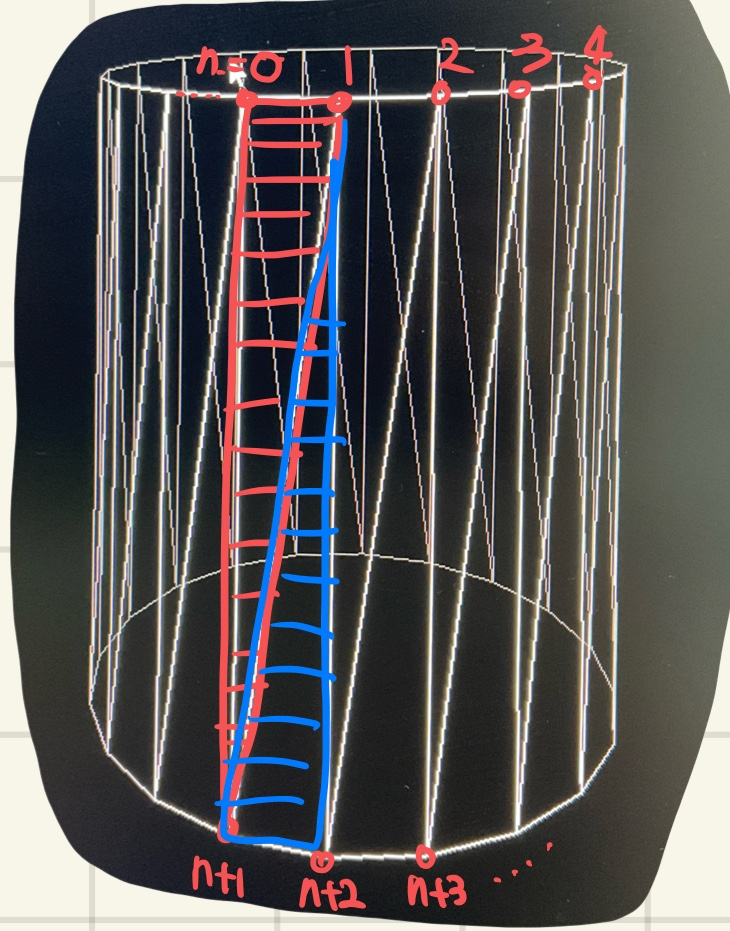
실린더의 경우 윗면의 버텍스들을 생성하고, 아랫면의 버텍스를 생성합니다.

그리고 indices를 0,1,n+1과 1,n+2,n+1과 같은 방식으로 삼각형 두 개를 렌더링합니다.

 

DirectX는 왼손 좌표계를 사용하기 때문에, z축 방향이 우리가 바라보는 방향입니다.

그래서 V0V1과 V0V2를 cross 했을때 노멀의 방향이 위 방향과 같아야 앞면으로 렌더링됩니다.
그럴려면 V0,V1,V2가 시계방향으로 ordering이 되어야 합니다.
이것을 clock-wise ordering 이라고 합니다.

무튼, DirectX에서 Indices를 시계방향으로 지정해줘야 사용자의 눈에 보이게 됩니다.

 

옆면 메쉬를 만드는 방식도 Quad와 큰 차이가 없습니다.

그러면 왜 갑자기 Cylinder mapping을 이야기 하느냐 하면, Cylinder로 sphere를 만들 수 있기 때문입니다.

 

1.3 Sphere 생성: Cylindrical way

Sphere를 어떻게 만드는지 생각해 보신적 있나요?

수학에서는 원점에서부터의 거리를 이용해서 구를 정의하지만, 이 방식은 수많은 점들이 필요하기 때문에

memory를 많이 사용하고, surface를 정의하기가 어렵습니다.

그래서 기존의 primitive를 변형해서 sphere를 생성합니다.

 

위 방식은 cylinder를 생성하는 방식에서 아이디어를 얻은 것입니다.

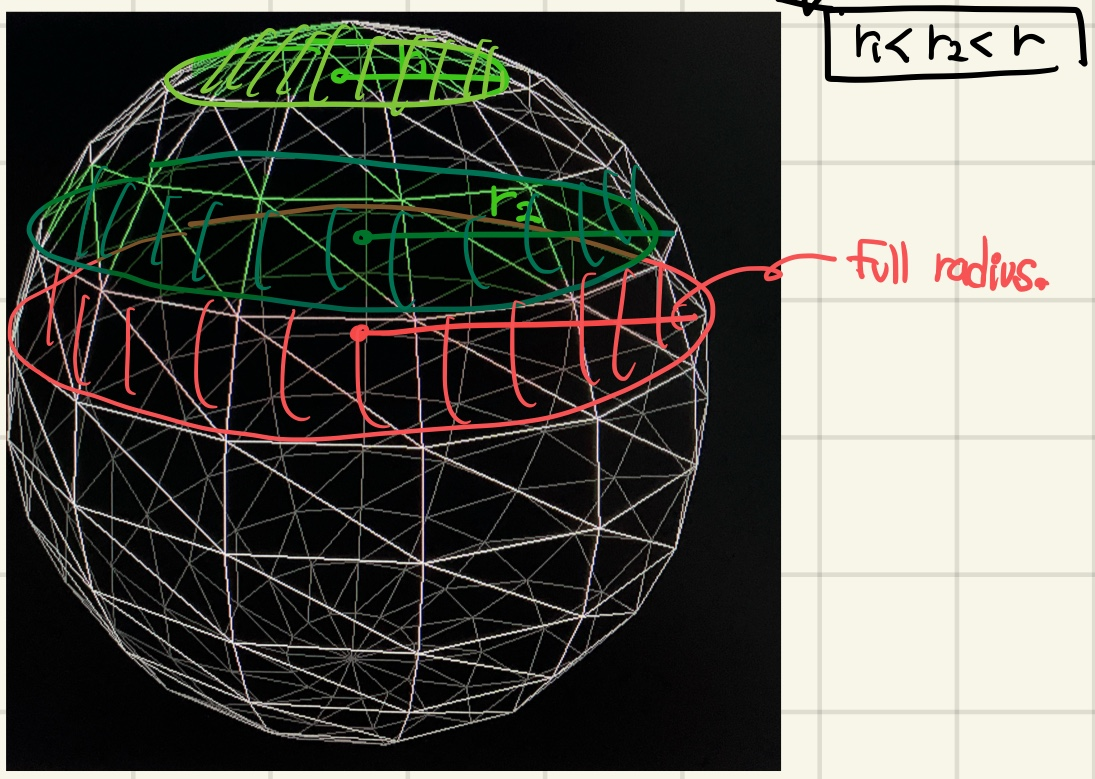
Cylinder를 생성하는 방식은, 마치 도자기를 만드는 과정과 비슷합니다.

반죽을 길게 늘어뜨린후, 한 층 한 층 감아서 쌓아 만듭니다.

Sphere는 여기서 각 층마다 쌓이는 cylinder의 radius를 변화시켜서 만듭니다.

텍스처를 입힌 모습입니다.

 

1.4 Subdivision을 사용하는 이유.

텍스처를 입혔을 때, 그럴듯 하게 보이는데 왜 이 방식말고 다른 방식을 사용할까요?

왜냐하면, mesh data가 memory를 너무 많이 차지하기 때문입니다.

위 sphere의 vertices와 indices 수를 출력했습니다.

indices가 더 많은 이유는, vertices는 삼각형을 만들 때 이미 중복이 되므로 재사용할 수 있지만,

indices는 재사용이 아니라 매번 다시 정의해야하기 때문입니다.

 

Subdivision을 사용한 경우, 기하급수적으로 mesh data가 줄어든 것을 볼 수 있습니다.

Subdivision 전의 Tetahedron의 모습입니다. 

Subdivision을 하면, 아래와 같은 모습이 됩니다.

Subdivision을 해도  vertices와 indices가 늘어나는데, 왜 subdivision을 하는지 궁금증이 생깁니다.

Subdivision은 cpu에서도 할 수 있지만, gpu에서도 수행할 수 있습니다.

gpu는 SIMD 구조이기 때문에 동일한 operation을 여러 data에 수행하는 데 강점이 있습니다.

그래서 subdivision을 gpu에서 수행하면, cpu에서 gpu로 meshData를 복사하는 시간을 줄일 수 있습니다.

 

 

 

2. Spherical Mapping

2.1 UV coordinates.

Spherical mapping의 경우, 구면상의 한 점의 좌표를 기준으로 texture map에서 u,v좌표를 계산합니다.

기존의 QUAD texture를 원에 빈틈없이 이어붙이는 것은 어렵습니다. 

세계지도를 지구본에 붙이는 과정을 생각해보면,

중심부는 팽창하고, 구의 pole(남극,북극이 되는 극점)에 갈 수록 왜곡이 커짐을 알 수 있습니다.

왜냐하면 2d 지도에서 동일한 영역이, 구에서는 훨씬 작은 영역에 들어가야 하니까, 일부 데이터가 탈락하는 일이 생깁니다.

 

결과적으로 중심부는 넓고, pole근처는 굉장히 작게 텍스처가 왜곡됩니다.

그래서 우리는 spherical coordinate를 도입해서, sphere위의 한 점으로부터 UV 좌표를 계산할 것입니다.

 

2.2 UV 계산

먼저 sphere위의 한 점은, Sphere coordinate를 이용해 표현할 수 있습니다.

Sphere coordinate에 익숙하지 않은 분들을 위해 설명하자면, 왼쪽 아래 그림에서 y축 기준으로 회전하는 angle을

phi라고 합니다. 이 과정에서는 radian angle을 기준으로 하기 때문에, phi의 범위는 2pi가 됩니다.

0~2pi범위의 phi를 2pi로 나눠주면, [0,1]범위로 바뀌는데, 이 것을 u로 사용합니다.

 

비슷한 방식으로 z축 회전각을 theta로 하면, theta는 [0,pi]범위가 됩니다.

마찬가지로 theta를 [0,1]범위로 바꿔주면 v가 됩니다.

 

2.3 Cartesian to Spherical Coord

그럼 문제는 Theta와 Phi를 찾는 문제로 바뀝니다. 하지만 우리가 가진 것은 Vertex Position이고, Vector3(x,y,z)로 표현됩니다. x,y,z 세 개의 축으로 구성된 좌표계를 Cartesian이라고 합니다. 반대로 theta와 phi를 이용해 점의 위치를 표현하면

이를 Spherical coord라고 합니다.

 

theta는 y/r인데, r=1로 두었습니다. phi는 z/x이므로 tangent angle이 됩니다.

acos를 이용하면 theta는 구할 수 있지만, atan2의 경우에는 약간의 문제가 생깁니다.

왜냐하면 atan2의 range가 [-pi.pi]인 반면에, phi의 범위는 [0,2pi]이기 때문입니다.

 

그래서 atan2(a,b)의 범위를 [-pi,pi] -> [0,2pi]로 변환해주는 작업이 필요합니다.

atan2의 정의에 따라서, 그림과같이 atan2(a,b)=atan2(-a,-b)+pi와 같습니다.

원래 atan의 range(치역)는 [-pi,pi]이므로 atan2(-a,-b)의 range는 [0,2pi]가 됩니다.

 

그런데 우리가 phi의 시작점을 다음과 같이 정의했습니다.

x가 처음에는 음수로 시작하는데, 우리가 tangent를 계산할 때는 sin/cos로 정의하므로 

atan2에서는 (z,-x)를 사용했습니다.

여기서 a,b를 -a,-b로 바꿔줘야하므로

 

결과적으로는 atan2(-z,x)+pi가 됩니다.

 

static void get_sphere_uv(const point3& p, double& u, double& v) {
        // p: a given point on the sphere of radius one, centered at the origin.
        // u: returned value [0,1] of angle around the Y axis from X=-1.
        // v: returned value [0,1] of angle from Y=-1 to Y=+1.
        //     <1 0 0> yields <0.50 0.50>       <-1  0  0> yields <0.00 0.50>
        //     <0 1 0> yields <0.50 1.00>       < 0 -1  0> yields <0.50 0.00>
        //     <0 0 1> yields <0.25 0.50>       < 0  0 -1> yields <0.75 0.50>

        auto theta = std::acos(-p.y());
        auto phi = std::atan2(-p.z(), p.x()) + pi;

        u = phi / (2*pi);
        v = theta / pi;
    }

code는 RaytracingNextWeek에 있습니다. 

위에서 설명한 내용과 동일합니다.

 

3. UV Seam issue

3.1 Mesh를 사용하는 이유

사실, Raytracing in one week에서 다룬 내용은 한 가지 문제가 있습니다.

바로 일반적인 complex mesh(복잡한 메쉬)에 대해서 uv seam issue가 생깁니다.

아티클에서는 mesh를 정의하지 않고, 대신에 수식을 이용해서 primitive를 정의합니다.

 

장점은 정확하게 primitive를 표현할 수 있다는 점입니다.

또한 cpu에서 gpu로 거대한 메쉬파일을 보내야할 일도 없습니다.

하지만 우리가 아는 일반적인 모델은, 수식으로 정의할 수가 없습니다.

그래서, 필연적으로 Mesh로 부터 Pixel Data를 생성하는 Rasterization이라는 과정을 거치게 됩니다.

그런데 이전과 다르게 uv를 매핑하는 방식에 문제가 생깁니다.

 

일반적인 모델의 경우 mesh에 uv가 이미 설정되어있기 때문에, 제공된 uv를 그대로 사용하면 문제가 없습니다만

subdivision과 같은 프로세스를 하게 되면, 메쉬의 수와 구조가 변하기 때문에 기존 uv를 사용할 수가 없습니다.

따라서 새로운 uv를 정의해 주어야 합니다.

 

3.2 Texcoord interpolation

다시 기존의 sphere example로 돌아가서 생각해 보겠습니다.

v.texcoord = (v0.texcoord+v1.texcoord)/2;

subdivision을 하는 경우, 기존 vertex v0,v1,v2에서 새로운 vertices v3,v4,v5를 생성합니다.

이때 v3 v4 v5의 texcoord는 기존 vertices.texcoord를 interpolation합니다.

 

이 방식은 대체로 잘 동작합니다만, 우리의 texcoord에는 한 가지 치명적인 문제가 있습니다.

 

3.3 UV Seam Issue

바로 uv=1.0에서 uv=0.0으로 넘어가는 지점입니다.

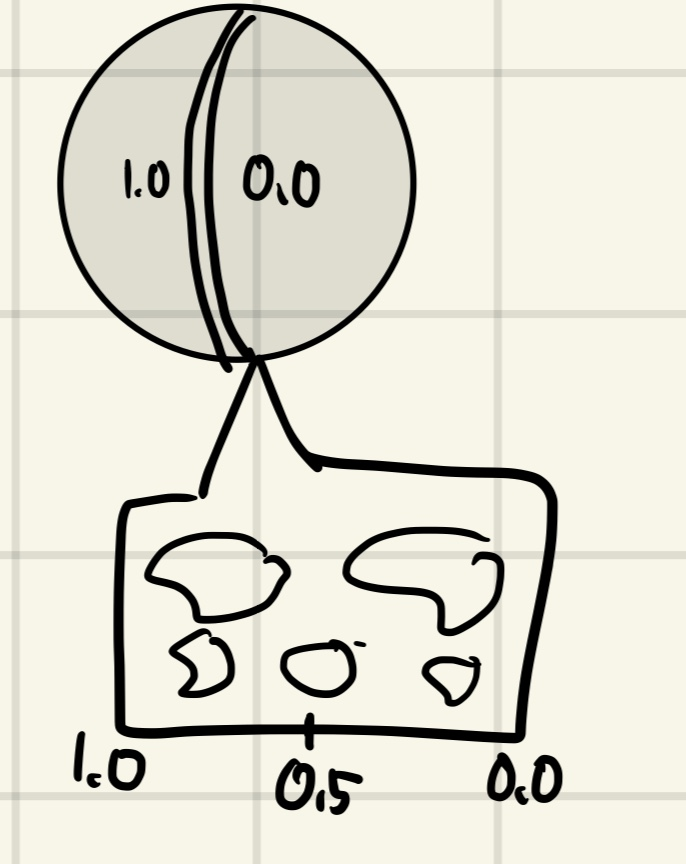
spherical coord를 사용하더라도,

phi=2pi -> phi=0이 되는 지점이 존재합니다.

이 지점에서 삼각형의 한 점은 u=1.0이 되고, 나머지 한 점은 u=0.0이 되는데,

이전에 언급한 방식으로 interoplation을 하면 삼각형의 중간지점은 u=0.5가 됩니다.

 

즉, 경계면에 텍스처 전체가 압축된 형태의 artifact가 생깁니다.

이것을 UV Seam이라고 합니다.

 

3.4 Solution

기존의 방식은 uv를 단계별로 증가시키고, 그리고 subdivision을 수행하는 방식입니다.

그래서 subdivision 수행 이후의 texcoord는 양쪽 vertex의 평균이 되기 때문에 texcoord의 변화가 크다면,

이를 해결하기가 어렵습니다.

 

그래서 subdivision 이후에 pixel shader에서 texcoord를 다시 계산하는 방식을 사용합니다.

float2 uv;
uv.x = atan2(input.posModel.z, input.posModel.x) / (3.141592 * 2.0) + 0.5f;
uv.y = acos(input.posModel.y / 1.5) / 3.141592;

x:phi angle, y:theta angle입니다.